風中一匹狼

先說我不會做太詳細的比較

畢竟我也不是專門分析資料庫的專業人士哈

這次分享主要是在使用者的角度討論這三個資料庫的使用心得

I. PubMed

Endnote目前更新到X9版本了

也是走最近的簡約風格，變美很多

如果不想每次都要手打一遍文獻這個軟體就會是個很好的助手

最近有種感慨，不是軟體不好，而是人不會使用而已

#在R執行SAS的glm lsmeans
#使用的資料為R內建的dataset- airquality
#可以先看一下該資料的描述(紐約某一年的空氣品質指標數據)
?airquality
head(airquality)

#輸出為csv檔供SAS使用
airquality$Month<- as.factor(airquality$Month)
write.csv(airquality, file = "airquality.csv")
 

#假設我們的實驗目的是要比較各月份的溫度是否有差異

#建立線性模型
#formula用於將Temp(反應變數)迴歸於Month(預測變數)，使用的資料為airquality
# day為類別變數# 把-1放在formula裏是不要讓截距項涵蓋在模型裏;
# 類別變數將自動地被設定成每個level都會有一個迴歸係數
Temp_lm<- lm(Temp~ Month -1 , data= airquality)
Temp_lm #結果顯示Intercept(截距項)和Month各類別的係數

Call:
lm(formula = Temp ~ Month - 1, data = airquality)

#資料處理技巧(2)
install.packages(c("magrittr","tidyr","dplyr"))
install.packages("tidyverse") #上面三個包都在其中
library(tidyverse)
cars %>% summary() #把cars叫進summary()。等同summary(cars) 
#應用運算符號%>%
birth<- 1995
age<- Sys.Date() %>%
  format(format= "%Y") %>%
  as.numeric() %>%
  `-` (birth)
#調整輸入位置
cars_lm<- lm(formula = dist~ speed, data= cars) #傳統方式
cars_lm<- cars %>%
  lm(formula = dist~ speed, data = .) #以. 指定資料輸入的位置

#gather() 將多個數值變數堆積在同一個數值變數中(value)，再用一個類別變數(key)紀錄數值變數的來源。
team_name<- c("Bull", "Warrior")
wins<- c(72,73)
losses<- c(10,9)
team<- data.frame(team_name,wins,losses)
team
gather(team, key = variable, value = values, wins, losses)

#filter() 篩選資料
filter(team, team_name== "Bull")
team[team_name=="Bull", ] #內建寫法

#select() 篩選特定變數
select(team, wins)
team[,"wins", drop= F] #內建寫法，drop= F為不轉為vector

#mutate() 新增衍生變數或非衍生變數
season<- c("1995-96", "2015-16")
mutate(team,
       winning_percentage= wins/(wins+losses),
       season= season)

#基因富集分析 (gene set enrichment set analysis)

#數據庫下載: 與自己的差異基因進行搜尋及比對
#AnnotationHub是生物數據庫的中轉站，方便搜尋目標數據，另一個相似套件為biomaRt
#參考網址:https://www.jianshu.com/p/ae94178918bc
source("https://bioconductor.org/biocLite.R")
install.packages("BiocManager")
BiocManager::install(c("AnnotationHub","BiocGenerics","parallel"))
library(AnnotationHub)
ah <- AnnotationHub()
ah

#版本是2018-08-20; 目前有45768條紀錄
unique(ah$dataprovider) #數據來源
unique(ah$species) #支持那些物種
ah$species[which(ah$species == "Gallus gallus")] #查詢Gallus gallus是否存在資料庫中
gallus <- query(ah, "Gallus gallus")
gallus #列出有 "Gallus gallus"這個物種的資料庫有哪些
ah[ah$species == "Gallus gallus" & ah$rdataclass == 'OrgDb'] 
subset(ah, species == "Gallus gallus" & rdataclass == 'OrgDb') #用R內建功能查詢有"Gallus gallus"且屬於'OrgDb'的數據庫
display(ah) #圖形化介面操作
deseq2.sig <- subset(res, padj < 0.05 & abs(log2FoldChange) > 1) #數據篩選，p<0.05，且log2>1
unique(ah$rdataclass) #AnnotationHub的註解訊息存放格式
gallus["AH61772"]
org_gal<-ah[["AH61772"]] #[[]]為下載數據庫，編號就是對應自己要搜尋的數據庫
str(org_gal)
mode(org_gal) #調查數據模式為S4
class(org_gal)
keytypes(org_gal);columns(org_gal) #搜尋可以輸入的基因名稱格式 (兩種函數皆可)

keys(org_gal,keytype = "ENTREZID") #查詢某一基因輸入格式有那些,keytype指定輸入格式
select(org_gal,keytype = "SYMBOL" ,keys= "ENO1", columns= c( "UNIGENE","GENENAME","ENTREZID","GO")) #從資料庫搜尋基因。
#key:關鍵字(須符合基因格式);column:欲列出的項目(格式)，一個基因有時會有多個GO

#GO分析
BiocManager::install("clusterProfiler") #使用富集分析會用到的package
library("clusterProfiler")
BiocManager::install("fgsea")
library(readxl) #可以讀入excel的package
# 以這組基因列表當練習: https://drive.google.com/open?id=1KTrQqok9cm5kPneo-Z8dWGEHaCNseUjp
#引用來源: https://www.sciencedirect.com/science/article/pii/S0306456518302456?via%3Dihub#f0020
#由於該文獻只有提供GI number，所以用DAVID的Gene ID Conversion Tool轉換成ENTREZ，不過原本有103個差異基因，轉換後只對的到70個
GO<-read_xlsx("GO.xlsx",col_names = T) #輸入資料，差異表達的基因 (ENTREZID命名格式)
BiocManager::install("enrichGO")
library(DOSE)
GO_BP <- enrichGO(gene         =as.character(GO$ENTREZ_GENE_ID), #輸入的基因列表需轉換成字元
                    OrgDb         = org_gal, #物種註釋數據庫，使用NCBI的database
                    keyType = "ENTREZID", #gene命名格式
                    ont= "BP", #選擇基因功能: 是BP (Biological Process), CC (Cellular Component), MF (Molecular Function)
                    pAdjustMethod = "BH",
                    pvalueCutoff = 0.05,
                    qvalueCutoff  = 0.2,
                    minGSSize = 10, #每個基因集最小數目
                    maxGSSize = 500, #用於測試的基因註釋最大數目
                    readable = FALSE, 
                    pool = FALSE)
write.csv(summary(GO_BP),"GO_BP.csv",row.names =FALSE) #寫出GO分類表格

#資料探索的檢定
#資料型態: 幾乎任何資料都可以拿來做資料探索，實務上，當變數數目跟觀測數都夠多時，資料探索的用處比較大。資料探索的目的為處理觀測值之間的交互關係，並將期間模式凸顯給實驗者。

#主成分分析和因素分析 (Principle component analysis (PCA) and factor analysis): 都是藉由加權變數來將每個個體的差異最大化。許多方面，主成分分析跟相關係數和回歸分析很類似。只要資料中每個個體都有兩個以上的觀測值就可使用。主成分分析假第資料是連續的且遵從常態分佈。若執行此分析的目的是為了建立新假設就可以忽略此假定。
#視覺化: 藉由「每個個體指有兩個觀測值」的特例將主成分分析的運作視覺化。想像將兩個相關的變數製成散佈圖，其資料形成橢圓形雲狀物。PCA會計算通過此橢圓形長軸的直線，並將此直線當成第一個主要軸線(PCA1)。通過資料雲，且和第一個軸線垂直的直線就是PCA2。分析過程是電腦以多維空間的形式進行，每個變數都代表一個維度，每條通過資料雲的直線都來自對於個變數做適當的加權。

PCA主成分分析原理及分析實踐詳細介紹 (很詳盡的介紹，也有R的演示)

#Example: 研究兩種果蠅物種，觀察資料包含五種型態的單位、性別和物種別。
sex<- c(1,1,1,1,2,2,2,2,1,1,1,1,2,2,2,2)
species<- c(1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2)
thorax<- c(1.01,0.98,1.02,1.05,0.98,0.89,0.89,0.95,1.20,1.15,1.18,1.21,0.95,0.94,0.96,0.91) #胸長
wing<- c(2.51, 2.45, 2.57, 2.61, 2.40,2.35, 2.38,2.41,3.10,3.12, 3.21, 3.20, 2.51,2.50,2.62,2.45) #翅長
femur<- c(.06,.05,.08,.07,.04,.04,.05,.05,.09,.10,.09,.10,.08,.07,.08,.07) #腿長
eye<- c(.52,.53,.55,.52,.54,.50,.50,.49,.48,.52,.52,.55,.56,.49,.51,.52) #眼距
ant<- c(.11,.12,.11,.10,.13,.14,.12,.12,.09,.10,.11,.09,.11,.13,.14,.13) #第三節觸角
data.frame(sex,species,thorax,wing,femur,eye,ant)
summary(prcomp(~thorax+wing+femur+eye+ant, scale= T)) #以prcomp()或princomp()皆可執行，結果也很相似，再來是定義主成分分析的變數(thorax, wing,femur, eye, ant)，但是分組變數不能輸入(species, sex)主成分分析中，最後加上「scale=T」讓個效果總合等於1。
#輸出結果顯示各主成分解釋多少比例的變異數: 「PCA1」解釋68.4%; 「PCA2」解釋19.8%

Importance of components:
                                       PC1    PC2     PC3       PC4       PC5
Standard deviation     1.8491 0.9941 0.61878 0.43913 0.12914
Proportion of Variance 0.6839 0.1976 0.07658 0.03857 0.00334
Cumulative Proportion  0.6839 0.8815 0.95810 0.99666 1.00000
print(prcomp(~thorax+wing+femur+eye+ant, scale= T)) #顯示各主成分中各變數項目的權重

#兩個變數之間有有因果關係嗎

#許多情況下，一組觀測值的取值很明顯是取決於另一組觀測值。本次的案例中每個「個體」都有兩個觀測值。一個觀測值是「原因變數」、「x變數」、「預測變數」、「自變數」，此變數的取值為實驗者的設定或選擇；另一個觀測值是「效果變數」、「y變數」、「應變數」，此變數的取值非實驗者設定。有一系列方式可以判斷原因和效果之間的關係形式和強度，每個方法對變數及其關係的假定各有不同，這裡考慮五種檢定: 線性回歸、Kendall最佳配適線、羅吉斯回歸、第二型模式回歸和多項式回歸。

#「標準」線性回歸: 即第一型模式回歸，是生物學中常用的統計模式，也是最常被濫用的統計方法，因為常忽略它的假定。線性回歸可判定兩個變數之間關係的形式和強度，很強大且有用。如果想要用給定x值(自變數)來預測y值(應變數)，就可運用。
#此檢定是在判斷斜率是否為0 (虛無假設b=0)，如果p< 0.05代表斜率和0有顯著差異，x和y變數之間有關係。
#線性回歸對資料有許多假定，包括x值沒有誤差;x值是由實驗者選擇或指定; x和y之間關係的最佳描述為一條直線 (y= bx); 不論x取值為何，y的變異數均相等，以及不論x取值為何，y均遵守常態分佈。
#Exmple: 研究實驗藥物的胃部吸收，試驗胃部的酸性程度是否會影響吸收。
uptake<- c(11.32,11.29,11.37,11.32,11.32,11.49,
           11.31,11.22,11.40,11.31,11.36,11.52,
           11.22,11.18,11.38,11.35,11.40,11.38,
           11.23,11.21,11.37,11.32,11.35,11.49)
pH<- rep(seq(from=0.6, to= 1.6,by=0.2),times= 4)
drug<- data.frame(pH,uptake)
summary(lm(uptake~pH)) #lm()可執行簡單線性回歸，輸出結果給出lm()的使用模型，報告殘差分布狀況；殘差為各點和擬和直線的垂直距離。最好的情況為殘差的分布是對稱的，且中位數是0。
#輸出的截距為X (pH)為0時y (uptake)的取值 (11.12695)，且和0有顯著差異。第二列給出關係的斜率 (0.19)和顯著性(0.000018)。這代表pH每增加1，uptake會增加0.19，且此斜率和虛無假設的0有顯著差異。
#R-squared為0.574，意謂反應變數(uptake)的變異數的57%可被預測變數(pH)解釋。

Call:
lm(formula = uptake ~ pH)

#檢定關係的檢定
#兩個變數之間有相關或相關性嗎?
#將資料中每次的觀測都賦予定性的值(如殼蛋的重量分級為"LL","L","M","MS","S")
#將觀測結果分類到各類別，即可運用檢定判斷觀測結果的類別是否獨立，可用的檢定有"卡方相關性檢定"、"phi係數"和"Cramér係數"

#卡方相關性檢定 (Chi-square test of association): 觀測結果可被分配兩個變數各自的組別中。本檢定並未對資料的形式限制，是一種無母數檢定，但卻沒有對應的母數分析。
#本檢定統計量為各類別組合的預期觀察數和實際觀測數的差值平方後，再全部相加。將此數值查卡方表，自由度為欄位數減一乘以列數減一。
#須注意 (1)預期觀察數不可小於1，應將各類別合併避免此問題 (2)預期觀測數小於5的比率應超過20%，若沒有提升到5以上的辦法，可改用Fisher精確性檢定。
#卡方檢定一定要用在頻率 (觀測次數)，不能用百分比或是轉換過的資料。統計結果會輸出統計量，自由度和P值的相關資訊。
#Example: 調查雞隻打架頻率是否和品種有關。在種雞場中隨機挑選了50隻雞作為定性調查。打架頻率被分為"低(L)"和"高(H)"，雞隻被分為四個品種(類別): "絲羽烏骨雞(Silkies)"、"竹崎(Shek-Ki)"、"花東(Hua-Tung)"、"金門(Quemoy)"。
chicken<- matrix(c(10,8,2,7,2,6,10,5),nrow=2,byrow=T, dimnames = list(c(1:2),c("Silkies","Shek-Ki","Hua-Tung","Quemoy")))
#虛無假設為兩種打架頻率的雞隻類別分配比例相等，意旨每個品種和某一打架頻率共同出現的機率相等。該檢定無法判定哪些類別組合比預期出現多還是少，不過可以直接檢視原始資料跟期望值大概就可得知。
chisq.test(chicken) #虛無假設被拒絕，回頭看原始資料可以發現Hua-Tung(花東)較常和打鬥頻率高有關。

#Cramér相關性係數 (Cramér coffecient of association): 和卡方檢定搭配、針對頻率表的檢驗。此係數提供有關相關性強度以外的資訊。χ2統計量用於判斷顯著性，Cramér係數(C)的絕對值則是取值0 (無相關)到1 (完全相關)，和樣本大小無關。可以用來比較相關性的程度。
#當表格為2X2時Cramér相關性係數就等於Phi係數 (每個變數僅有兩個類別)，Phi係數為卡方值除以總觀測數後後開根號
x<- matrix(c(10,2,8,6), nrow=2)
a<-x[1,1]; b<-x[1,2]; c<-x[2,1]; d<- x[2,2]
e<-x[1,1]+x[1,2]; f<-x[2,1]+x[2,2]; g<-x[1,1]+x[2,1]; h<-x[1,2]+x[2,2]
phi<- ((a*d)-(b*c)) / (sqrt(e*f*g*h))
phi

#觀測值結果賦予一個實際數值: 每次的觀測各付兩個變數一個實際有意義的值，族有一些檢定可以判斷這兩組觀測值是否有相關性、其關係強度、和此相關性是否顯著。有四種檢定可使用: Pearson積差相關、Spearman序位相關、Kendall序列相關、回歸。
#「標準」相關 (Pearson積差相關): 此檢驗產生的數值r是用來估計真實的相關係數 ρ (rho) 。取值從-1到1，代表完全負相關到完全正相關。使用條件為兩個變數均須為連續尺度，且均為常態分佈，若這些假定不成立則興改成Spearman序列相關。
#Example: 調查荷蘭牛每日食用飼糧的重量(kg)，共有六對牛，虛無假設為公母牛的食量沒有相關。兩個變數都遵從常態分佈。
Holstein<- matrix(c(17.1,16.5,18.5,17.4,19.7,17.3,16.2,16.8,21.3,19.5,19.6,18.3), ncol = 2, byrow = T,
                  dimnames= list(c(1:6),c("female","male")))
Holstein<- as.data.frame(Holstein)
Holstein$pair<- c(1:6)
Holstein<- data.frame(pair= Holstein$pair, female=Holstein$female,male= Holstein$male)
cor(Holstein[,"female"],Holstein[, "male"])
cor(Holstein$female,Holstein$male)^2 #r^2為0.77
cor(Holstein) #可把所有變數組合的相關係數輸出
cor.test(Holstein$female,Holstein$male) #該指令可輸出更多結果跟P值，結果確認0.8相關係數確實顯著，P值為0.02，r的信賴區間為0.24-0.98。代表雌性和雄性的食量很可能呈正相關。

#Spearman序列相關 (Spearman's rank order correlation): 為「Pearson積差相關」對應的無母數檢定版本之一。輸出的統計量稱為rs，取值也是-1到1，雖然看起來跟Pearson的r相同，但不建議直接拿來跟r比較。只要同一個體有兩個觀測值，這些觀測值的測量尺度可以有意義的被排序。該相關比Pearson保守許多。
#Example: 使用跟上題一樣的資料
cor(Holstein$female, Holstein$male, method = "spearman")
cor.test(Holstein$female,Holstein$male, method = "s") 
cor(rank(Holstein$female), rank(Holstein$male)) #使用rank可以驗證是否得到相同結果，也可以發現Spearman就是排序資料的Pearson相關。

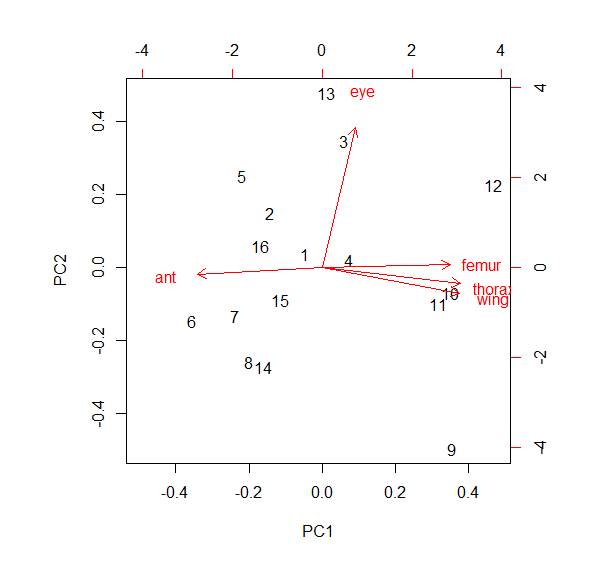
#資料有大於兩種互相獨立的分組方法

#多因子檢定 (Multifatorial testing): 需分析因子數越多，需要分析的交互作用項也會快速增加。
#三因子變異數分析 (無重複試驗) [Three-way ANOVA (without replication)]
#Exzample: 白羅曼鵝的性別、受日照長短、試驗區域對其採食量影響
intake<- c(78.1,76.3,
           69.5,73.2,
           82.4,83.0,
           72.3,70.0)
sex<- rep(c("F","F","M","M"),times= 2)
light<- c("L","L","L","L","S","S","S","S")
region<-c("A","B","A","B",
          "A","B","A","B")
data.frame(intake=intake, sex=sex, light=light,region=region)
summary(aov(intake~sex*light*region))
summary(aov(intake~sex*light*region-sex:light:region)) #為無重複試驗時須要扣除同時有三因子之交互作用 (-sex:light:region)

#三因子變異數分析 (有重複試驗) [Three-way ANOVA (with replication)]
#使用條件: (1)資料有三種完全獨立三種方法 (2)每個因子組合都有超過一個觀測值 
#檢定的假設: 資料是連續、趨近常態分佈、每個因子變異數相等，如果資料不滿足以上假設，此檢定並沒有對應的無母數版本
#Example: 觀察牛群放牧對周遭牧草生長的影響。分別在兩個地點(I,II)，兩個時間(白天(D)和黑夜(N))試驗，每個地點有6個取樣點，分成ABC三種，其中2個點作為控制組 (不做任何處置)，2個點用柵欄圍起來不讓牛隻進入，最後兩個是程序控制組 (仍讓牛隻進入，但有實施柵欄工程)，該試驗必須設置程序控制組，否則效果只能被歸因於牛隻進入或柵欄工程。觀測值為牧草的生長量，以下是觀察資料。
grass<- c(112,115,187,141,121,189,121,145,198,135,141,208,
          116,102,175,101,157,186,138,124,168,129,133,206)
place<-rep(c("I","I","I","I","I","I","II","II","II","II","II","II"), times=2) 
time<- rep(c("D","D","D","N","N","N","D","D","D","N","N","N"), times=2)
treatment<- rep(c("A","B","C","A","B","C","A","B","C","A","B","C"), times=2)
data.frame(place,time,treatment,grass)
model<- aov(grass~ place*time*treatment) #有一個主效果顯著，另外兩個接近顯著，所有的交互作用皆不顯著
summary(model)
TukeyHSD(model, "treatment") #事後檢定採樣點(ABC)中，哪幾個水準互相有差異

#多因子變異數分析 (Multiway ANOVA): 多於三組的分類因子，每種因子均互相獨立
#困難點：(1)隨著因子數目增加，交互作用項也會急速增加，導致解讀困難 (2)因子數變多，其之間獨立的機會也會降低
#考慮與解決: (1)真的每個因子都獨立嗎? (2)是否某些因子可以合併 (3)是否鑲嵌在其他因子 (4)使用共變數的方式分析

#分組方法並非都是獨立: 很多實驗會認為因子互相獨立，在研究後才發現不全然是，因此考量分析中各因子間的獨立性是重要的
#非獨立因子: 有些資料分子是固定的，像是性別來做作主效果因子。但可能其他因子就會變得不固定，舉例來說，依照性別分組後再依照體重重或輕來分組的話會發生體重較重的組別男性會比女性多，因此這個因子(性別男和女、體重輕和重)並非獨立。這種相依性可以用卡方關聯性檢定來檢驗。
#因子不獨立的話就不適合作因子變異數分析，解決方式是把性別當作固定因子，體重作為共變數執行共變數分析。

#屬性資料的分析

#擲兩個骰子，兩個骰子的點數一樣的機率為多少?兩個骰子總共點數不足5的機率為多少
dbinom(2, size = 2, prob = 1/6)*6
first<- (1:6) ;second<- (1:6)
results<- c()
i<-1
while (length(results) < 100000) {
  results[i] <- (sample(first , 1)+ sample(second,1)) <5
  i<-i+1
}
sum(results)/100000

#為了檢定一個虛擬假說，進行四次試驗(互相獨立)。如果虛擬假說是正確的，至少得到一次顯著的結果 (p< 0.05)的機率有多少?
1-dbinom(4,size = 4, prob = 0.95)

#一群乳牛乳脂率低於4%佔60%，如果隨機取10頭牛，其中剛好6頭牛的乳脂率低於4%的機率有多少?
dbinom(6, size = 10, prob = 0.6) #取樣10次，其中6次成功(< 4%)的機率
#至少有4頭牛之乳脂率大於或等於4%的機率 (也就是1-成功三次以內的機率)
1- pbinom(3, size= 10, prob = 0.4) #>=4%的機率為0.4，累積成功3次的機率，100%扣除該機率

#動物藥品聲稱對某疾病有90%治癒率，使用於10頭病畜，治癒8頭。此藥是90%治癒率嗎? 以二項分布與常態近似法測定，結果是否不同? 哪種方法才是正確
#二項分布
1- dbinom(10,10,0.9)- dbinom(9, 10, 0.9) #至少治癒8頭機率為0.26，並沒有足夠證據拒絕治癒率低於90%
#常態近似法
p<- 0.9
pnorm(8, mean= 9, sd= sqrt(10*p*(1-p))/0.5) #標準偏差除以0.5校正連續性。
#常態近似法與二項分布算出的機率有些差異是因為P在接近1 (90%)且樣本數少的情況下，二項分布是有些傾斜不像常態分不一樣對稱。在該情境下二項分布會比較適用。
#http://episte.math.ntu.edu.tw/articles/sm/sm_16_07_1/index.html poisson分布介紹